The Value of Attack and Defence

TL;DR

The value of a combatant is sqrt(attack x defence)

Introduction

The rules for combat in many role-playing and war games are quite similar. Opposing teams (made up of several fighters) fight until the other is destroyed.

Fighters inflict damage on each other by attacking. They can suffer a limited amount of damage before dying (or fleeing, or some other equivalent).

We can give each combatant an Attack Score (how much damage they inflict, on average, over time). Something like 10 damage per turn or 4.5 damage per second. We can also give them a Defence Score (how much damage they can suffer before dying).

If we want the game to be fair, or at least know which team is likely to win, we need some way of measuring the value of each fighter.

The Game

In most combat games, fighters can attack over distances, expend special abilities, use formations, and so on. It is either impossible, or impractical, to calculate the exact value of a fighter. We might calculate it, statistically, by simulating combat a few thousand times.

However, by looking at simplified combat games, we can make some useful insights.

For now, we’ll assume all fighters attack simultaneously, so we can ignore the advantage gained by attacking first. Our insights will still apply to games where attacks are not very damaging, or most fighters have roughly the same chance of attacking first.

We’ll also assume fighters can distribute their damage any way they want:

1. Fighters with high Attack scores cannot hide behind fighters with high Defence scores (we’ll consider this situation later). Either most fighters have similar proportions of Attack to Defence, or cannot avoid attacks through distance or positioning.
2. Fighters can divide their attacks between multiple targets (so an attack that inflicts 10 damage is not wasted against units with Defence scores of 1)

We’ll also assume teams’ total Attack scores decrease proportionate to how much damage they have suffered. This will make our insights inaccurate for games where some teams’ fighters can survive significantly more attacks than others (and thus those teams’ total Attack scores are diminished less frequently).

Wow, that’s a lot of assumptions – but we need to start somewhere. And now we can calculate the value of each fighter…

The Maths

All I’ll say about the convoluted dead-ends I explored while figuring this out is that if you produce the following with an automatic equation solver, you’re doing it wrong:

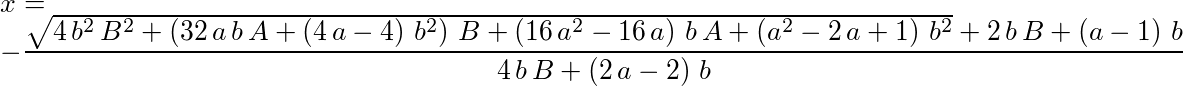
We can find the (correct) equation with fairly basic maths. Let’s define some variables:

A_X

The average Attack Score of each fighter in team X

D_X

The average Defence Score of each fighter in team X

N_X

The number of fighters in team X Logically, this is equal to B_X / V_X.

V_X

The average value of each fighter in team X

B_X

The total budget (value) of team X

Given the assumptions made earlier, we know that the team which suffers the most damage (as a proportion of their total Defence) in the first turn (or minute, or whatever) of combat is weakest.

In the first turn, the damage suffered by Team 1 (versus Team 2) proportionate to its total Defence score is:

(N₁D₁ – N₂A₂) / N₁D₁

Thus, in a fair fight:

(N₁D₁ – N₂A₂) / N₁D₁ = (N₂D₂ – N₁A₁) / N₂D₂.

Getting rid of the denominators:

N₂D₂N₁D₁ – N₂D₂N₂A₂ = N₁D₁N₂D₂ – N₁D₁N₁A₁

D₂A₂(N₂)² = D₁A₁(N₁)²

Substituting NX for 1/VX (this is a fair fight, so each team has the same budget, which we’ll set at 1):

D₂A₂ / (V₂)² = D₁A₁ / (V₁)²

(V₁)² / (V₂)² = D₁A₁ / D₂A₂

Thus:

(V_X)² = D_XA_X V_X = square root of D_XA_X